sitenevada.blogg.se - Chain rule calculus

#Chain rule calculus how to
#Chain rule calculus full
#Chain rule calculus android
#Chain rule calculus series

Partial derivatives are found when in the differentiation of any function one or more variable is kept constant with respect to the differentiating variable. The chain rule is an important derivative rule that allows us to work with composite functions. We use sign diagrams of the first and second derivatives and from this, develop a systematic protocol for curve sketching. This module continues the development of differential calculus by introducing the first and second derivatives of a function. The chain rule provides us a technique for finding the derivative of composite functions, with the number of functions that make up the composition. The chain rule is very useful when you need to.

#Chain rule calculus how to

The concept of chain rule also works for partial derivatives. Properties and applications of the derivative. Join 23K views 3 years ago New Calculus Video Playlist This calculus video tutorial explains how to find derivatives using the chain rule. cos 2x Chain Rule for Partial Derivatives f(x) = p, then its derivative is given as, Now for any three functions p, q, and r and a composite function f where f is a composite of p, q, and r such that, f = (p o q) o r, i.e. the nesting of function occurs, chain rule of differentiation fails in such a situation double chain rule is applied.

ISRO CS Syllabus for Scientist/Engineer Examįor a function where it is dependent on more than one variable.

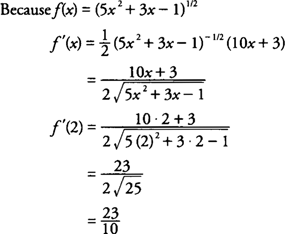
ISRO CS Original Papers and Official Keys.GATE CS Original Papers and Official Keys.DevOps Engineering - Planning to Production.Python Backend Development with Django(Live).

#Chain rule calculus android

Android App Development with Kotlin(Live).

#Chain rule calculus full

Full Stack Development with React & Node JS(Live).

Java Programming - Beginner to Advanced.

Data Structure & Algorithm-Self Paced(C++/JAVA).

Data Structures & Algorithms in JavaScript.

#Chain rule calculus series

Data Structure & Algorithm Classes (Live) Visualizing the chain rule and product rule Chapter 4, Essence of calculus 3Blue1Brown 5.01M subscribers Subscribe 1.5M views 5 years ago 3Blue1Brown series S2 E4 A visual explanation of what.

Which represents the slope of the tangent line at the point (−1,−32). A technique that is sometimes suggested for differentiating composite functions is to work from the “outside to the inside” functions to establish a sequence for each of the derivatives that must be taken.Įxample 1: Find f′( x) if f( x) = (3x 2 + 5x − 2) 8.Įxample 2: Find f′( x) if f( x) = tan (sec x).Įxample 5: Find the slope of the tangent line to a curve y = ( x 2 − 3) 5 at the point (−1, −32).īecause the slope of the tangent line to a curve is the derivative, you find that Its position at time t is given by s(t) sin(4t).

What is the velocity of the particle at time t 6 Checkpoint 3.39 A particle moves along a coordinate axis. Its position at time t is given by s(t) sin(2t) + cos(3t). Here, three functions- m, n, and p-make up the composition function r hence, you have to consider the derivatives m′, n′, and p′ in differentiating r( x). Using the Chain Rule in a Velocity Problem A particle moves along a coordinate axis. If a composite function r( x) is defined as Note that because two functions, g and h, make up the composite function f, you have to consider the derivatives g′ and h′ in differentiating f( x). For example, if a composite function f( x) is defined as The chain rule provides us a technique for finding the derivative of composite functions, with the number of functions that make up the composition determining how many differentiation steps are necessary. Volumes of Solids with Known Cross Sections.Step 1 Differentiate the outer function, using the table of derivatives. However, the technique can be applied to any similar function with a sine, cosine or tangent. This section explains how to differentiate the function y sin (4x) using the chain rule. Second Derivative Test for Local Extrema The chain rule in calculus is one way to simplify differentiation.First Derivative Test for Local Extrema.Differentiation of Exponential and Logarithmic Functions.Differentiation of Inverse Trigonometric Functions.Limits Involving Trigonometric Functions.